A word to the faint of heart: brace yourselves! Twisting and turning, you will traverse various, potentially dangerous grids as you trace dragons and other beauties on a turtle's back!
Our main motivation is to make these curves more popular, because they deserve it.
Here you can find some basic information about the mathematics behind the curves, taken from Julia Handl’s and Joerg Arndt’s publication “Fractal Plane-filling Curves” [1] and Joerg Arndt’s „Plane filling curves on all uniform grids” [2]. You can find our publications on this topic here.
Plane-Filling Curves

Plane-filling curves have been known for many years, starting in 1890. Famous examples are the ones described by Hilbert and Peano [3, 4].
A plane-filling curve is a curve that fills a part of the plane completely and until 2013 only a few of them were known. The curves we consider here live on certain grids, just like the Hilbert-curve and the Peano-curve.
Then Joerg Arndt started his search for all curves of a specific class. He succeeded – and found about a million new ones!
LINDENMAYER-SYSTEMS (L-systems)
Lindenmayer-systems were introduced in 1968 by the biologist Aristid Lindenmayer. Their original purpose was to create a theoretical framework for studying the development of simple multicellular organisms. We use the simplest Lindenmayer-systems, the ones containing only one non-constant symbol, to represent the curves in our class. L-systems are deterministic text replacing automata. In the following example, we replace the letter F with the word F+F-F. Both + and – are mapped to themselves. The order of the curve, which is the number of letters F in the word, is 3.

The figure shows how the first F, a simple stroke, is replaced by the word F+F-F. This shape is the first iterate of the L-system. In the next iterate, every F is again replaced by the word, + and – remain unchanged.

The rendering of the curves is done using turtle graphics. F is interpreted as “draw a line in the current direction”, + and – are interpreted respectively as turns by ± 120° (since the underlying grid consists of triangles). On other grids, turns by 60°, 90° or 120° are possible. The resulting curve is well known, it’s the terdragon that was described by Davis and Knuth [5].
THE GRIDS
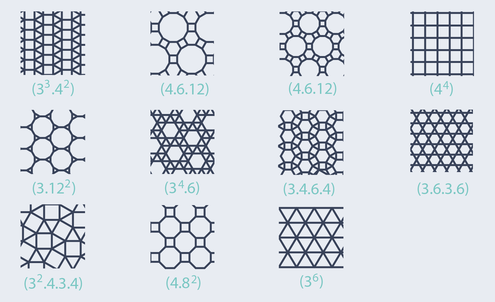
As mentioned earlier, we consider curves on certain grids. The plane-filling curves in our class can only exist on grids that have an even number of indices at each point. Hence the curves can be found on the triangular grid, the square grid and the tri-hexagonal grid. Thus, the hexagonal grid with three edges meeting at every point is out of the question.
There are more grids that we are interested in. They are called uniform grids and they already contain the triangular, square, hexagonal and tri-hexagonal grid. The symbol for the grid is the list of numbers of the edges of the polygons around a vertex in order of the least cyclic shift [6].
PROPERTIES OF THE CURVES

The curves we focused on in the search have the following properties: they are self-avoiding and edge-covering (EC). That means they never cross themselves and they traverse each edge of the underlying grid once. Curves that traverse every point of a grid once can be obtained from edge-covering curves by transformations that we found. In [1] and [7] you can find constructions for point-covering (PC) curves on all grids under consideration.
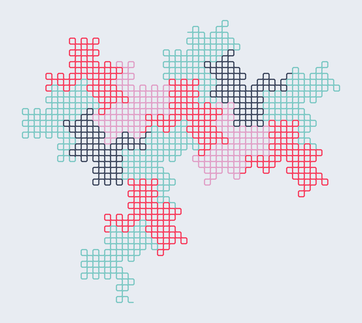
Every curve has two corresponding tiles. Three copies of the curve are assembled into a form that looks like a snowflake. The other tile looks more like a triangle. The curves are self-similar. As you can see in the next figure, the curve of order 13 living on the triangular grid is divided into 13 smaller rotated and scaled copies of itself.

[1] Julia Handl, Joerg Arndt: Fractal Plane-filling Curves, in Jürgen Mottok, Marcus Reichenberger, Reinhard Stolle (Eds.), ARC Conference Proceedings, pp. 248-251, (2016).
[2] Joerg Arndt: Plane filling curves on all uniform grids, on arxiv.org, (2016)
[3] Giuseppe Peano: Sur une courbe, qui remplit toute une aire plane, Mathematische Annalen, vol. 36, no. 1, 1890.
[4] David Hilbert: Ueber die stetige Abbildung einer Linie auf ein Flächenstück, Mathematische Annalen, vol. 38, 1891, pp. 459-460.
[5] Chandler Davis, Donald E. Knuth: Number representations and dragon curves, in: Selected Papers on Fun and Games, CSLI Publications, 2011, pp. 571-614.
[6] Branko Grünbaum, Geoffrey C. Shephard: Tilings by regular polygons, Mathematics Magazine, vol. 50, no. 5, 1977.
[7] Joerg Arndt, Julia Handl: Plane-filling Curves on Grids, in Bridges Math Art Proceedings, pp. 537-540, (2016).
